作业设计
教 材 上海九年义务教育课本 初一 第一学期 (试用本)
课 题 9.14(1)平方差公式
一.课堂训练
试 题 | 解 答 | 设计意图 |
A组 1.下列多项式可以用平方差公式分解因式吗?假如可以,请分解因式: (1) (2) (3) (4) (5) (6)
| 解: (1)不可以 (2)能
(3)能
(4)不可以 (5)能
(6)不可以 |
对可以用平方差公式因式进行因式分解的多项式的特征进行巩固. |
2.分解因式: (1) (2) (3)
| 解: (1)原式 (2)原式
| 遵循学生的认知规律,由浅入深,按部就班,让学生领会到公式中
|
B组 1.分解因式: (1) (2) (3) (4) (5) (6)
| 解 (1)原式
(2)原式
(3)原式
(4)原式
(5)原式
(6)原式
| 综合运用提公因式法和平方差公式进行分解因式,分解时学生应该注意两点:第(1)(2)(3)(4)(6)题中应该注意有公因式时,一般要先提取公因式;第(5)题因式分解结果要分解到不可以再分解为止. |
2.方便办法计算: (1) (2) | 解: (1)原式= = =
| 运用平方差公式进行方便计算,领会平方差公式有哪些用途,激起学生的兴趣. |
3.如图,已知
| 解:
当
答:圆环的面积约为 | 在实质问题的应用中,借助平方差公式分解因式使计算得以方便,领会平方差公式有哪些用途,增强学生学数学用数学的意识. |
C组 1.把一张如图甲形状的纸剪拼成图乙形状的长方形,作为一幅精美剪纸的衬底,你觉得如何剪拼?你可以用数学常识讲解吗?
甲 乙 |
解:
| 用几何图形验证平方差公式. |
二.课后作业
试 题 | 解 答 | 设计意图 |
A组 1. 将多项式 (A) (B) (C) (D) | 答:(C) | 进一步认识平方差公式的特征. |
2.将下列各式表示成平方的形式: (1) (2) (3) (4) (5) (6) | 答: (1) (3) (5) | 练习将数、式化为平方的形式,为后面运用平方差公式分解因式做好变式筹备.
|
3.分解因式:
(1) (2) (3) (4) (5) (6)
| 解: (1)原式 (2)原式 (3)原式 (4)原式 (5)原式 (6)原式 | 遵循学生的认知规律,由浅入深,按部就班,正确领会平方差公式的特征,让学生领会到公式中
|
B组 1.借助平方差公式计算: (1) (2) (3)
|
(2)原式
(4)原式
| 练习灵活运用平方差公式方便计算,领会平方差公式有哪些用途,激起学生数学的兴趣. |
2.分解因式: (1) (2) (3) (4) (5)
(8) (9) 补充)
| 解: (1)原式 (2)原式 (3)原式 (4)原式
(5) 原式 (6)原式
(7)原式
(9)原式 | 综合运用提公因式法和平方差公式进行分解因式. 第(1)、(4)、(6)、(7)、(8)题中应该注意有公因式时,要先提取公因式,再运用平方差公式分解因式; 第(2)、(8)题因式分解结果要分解到不可以再分解为止; 第(3)、(5)、(6)、(7)题,让学生领会到公式中 |
| 解:设大圆半径为
当
答:圆环的面积约为 | 在实质问题的应用中,借助平方差公式分解因式使计算得以方便,领会平方差公式有哪些用途,增强学生学数学用数学的意识. |
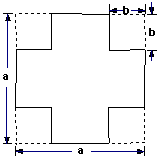
C组 1.已知一块“十字型”纸板如甲图,乙图是一个面积和甲图面积相等的长方形,你可以用数学常识讲解吗?
甲图 |
乙图
| 依据图中两个图形等积变换,进一步验证平方差公式,使用图形变化来激起学生学习兴趣,体现数形结合的数学思想. |
2. 你能说明
| 解:能
= = = 答:由于式子 | 灵活运用平方差公式讲解整除问题. |




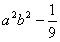
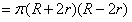


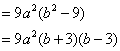





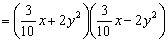




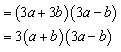
 3.如图是一个机器零件的截面,大圆的半径为
3.如图是一个机器零件的截面,大圆的半径为